Have you ever been curious about how your brain works? The brain is a high-dimensional, multi-scale, nonlinear dynamical system of combinatorial complexity, arising from billions of neurons with convoluted connections among them. To develop effective mathematical theories to describe its function is a deep intellectual challenge, wherein lies the inspiration of the research in our group. In general, the research in our group attempts to exploit mathematics to understand the computations of the brain. In particular, we are interested in constructing mathematical theories to explain the mechanisms underlying brain activity at multiple scales -- from a single neuron to neuronal networks, developing statistical methods to extract information from experimental data, and proposing theoretical frameworks for the computation carried out in various brain areas.
The research in our group focuses on the mathematical theory of single neuron computation and the dynamics and function of neuronal networks. We use mathematical modeling, theoretical analysis, and numerical computation to study scientific problems arising from neuroscience. As applied mathematicians and computational neuroscientists, we are in quest of mathematical understanding of brain computation with its quantitative verification in close collaboration with experimental laboratories. Below we introduce some projects and scientific questions that we are currently working on.
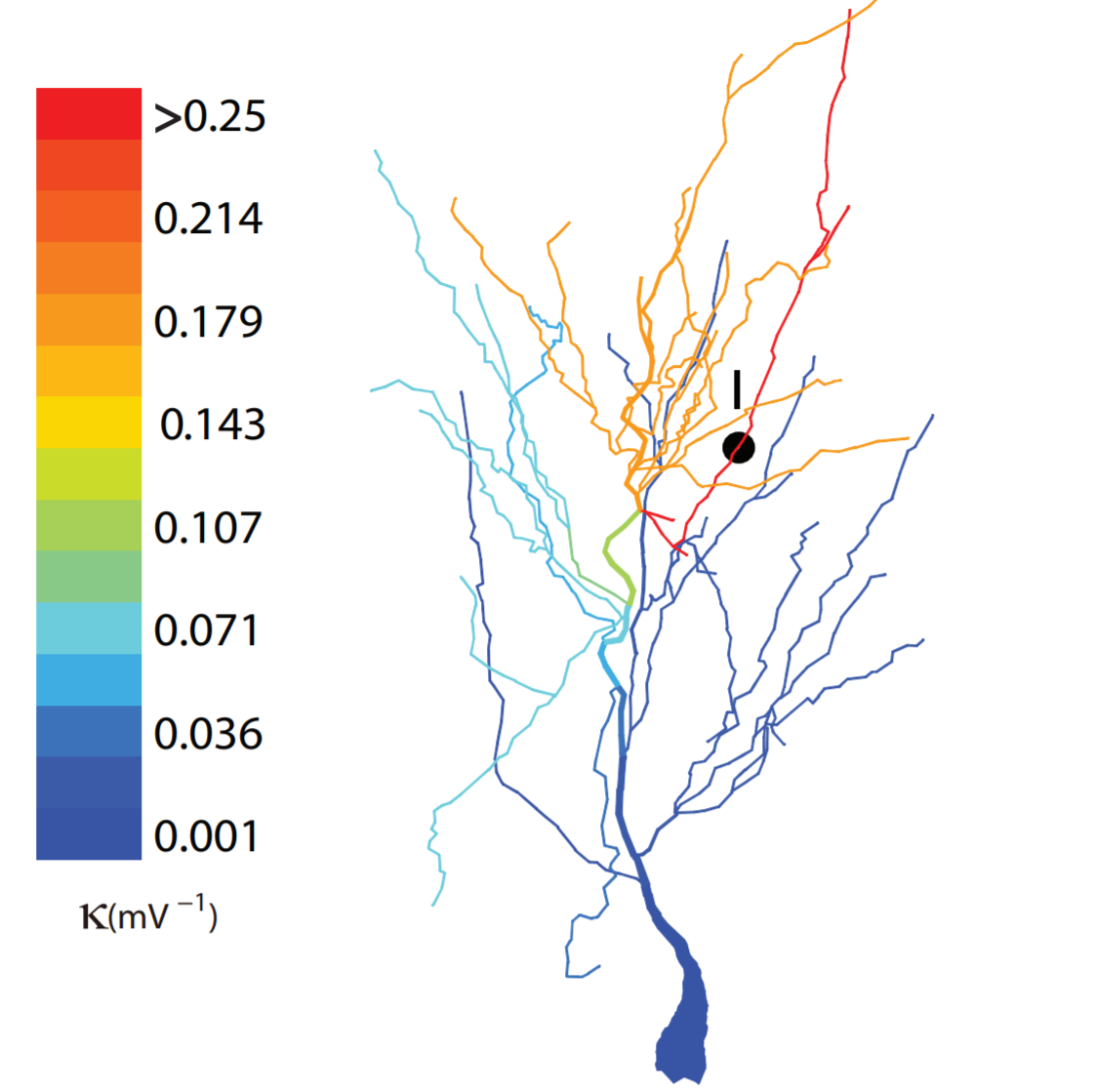
Single neuron computation. Neurons are basic computational units in our brain. To understand how the brain works, it is crucial to understand how a neuron computes as an initial step. For instance, how do neurons integrate synaptic inputs? What kind of computations are performed by neuronal dendrites? Can we develop simplified neuron models that are capable of capturing dendritic computations? What is the role of plasticity in neuronal computation? Is it possible to recover local and effective synaptic conductances in the presence of the space-clamp effect?

Network structure, dynamics, and function. The comprehensive structural connectivity of microscopic neuronal circuits and macroscopic multi-regional cortical networks empowers rich dynamics and functions of the brain. Yet quantative relations among cortical network structure, dynamics, and function remain largely unknown. For instance, how does heterogeneous connectivity structure give rise to network activity such as oscillations, waves, and excitation-inhibition balanced state? How are signals reliably propagated in cortical networks? Is it possible to recover the structural connectivity from the activity of neurons or brain regions?

Brain-inspired machine learning. Despite that machine learning has achieved a great success in scientific research and industrial applications, it remains to encounter problems including generalization ability and energy efficiency. However, these problems have already been solved by the brain. Therefore, it is promising to develop brain-inspired artificial intellegence in order to further improve the performance of today's machine learning algorithms. For instance, how to incorporate the computational ability of dendrites, the spiking dynamics of neurons, and the connectomic structure of cortical networks into the design of brain-inspired machine learning algorithms?
We are currently looking for highly-motivated undergraduates, graduates, postdocs, and visiting research students who are passionate about exploring the brain using mathematical and physical approaches. If you are interested in joining us, please send an email to songting at sjtu.edu.cn.